Colbyn's School Notes
Meta
Miscellaneous
Functional Utilities & Notation Conveniences
Right to Left Evaluation
$$\begin{equation}
\begin{split}
f \triangleleft x &= f(x)
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
f \circ g \triangleleft x
&= f(g(x)) \\
&= f \triangleleft g \triangleleft x
\end{split}
\end{equation}$$
Left to Right Evaluation
$$\begin{equation}
\begin{split}
x \triangleright f &= f(x)
\end{split}
\end{equation}$$
Derivative Shorthand
$$\begin{equation}
\begin{split}
\delta f(x) &= \frac{\mathrm{d}}{\mathrm{d}x} f(x) = f^\prime(x)
\end{split}
\end{equation}$$
For this notation, the derivative with respect to a given variable, is implicit.
Radians & Radian Conversion
Constants
$$\begin{equation}
\begin{split}
\tau &= 2\pi = 360^{\circ} \\
\pi &= \frac{1}{2}\tau = 180^{\circ}
\end{split}
\end{equation}$$
Conversion
$$\begin{equation}
\begin{split}
\text{Given}\\
\textcolor{blue}{1}^{\circ} &= \frac{\textcolor{blue}{1}}{360} \tau \; {\displaystyle {\mathrm{rad}}} \\
\textcolor{blue}{1} \; \mathrm{rad} &= \frac{\textcolor{blue}{1}}{\tau} \cdot 360^{\circ} = \textcolor{blue}{1} \cdot \frac{360^{\circ}}{\tau} \\
\\\text{Degrees to Radians}\\
\textcolor{blue}{x^{\circ}} &= \frac{\textcolor{blue}{x}}{360} \tau \; {\displaystyle {\mathrm{rad}}} \\
\\\text{Radians to Degrees}\\
\textcolor{blue}{x} \; \mathrm{rad}
&= \frac{\textcolor{blue}{x}}{\tau} \cdot 360^{\circ} \\
&= \textcolor{blue}{x} \cdot \frac{360^{\circ}}{\tau} \\
&= \textcolor{blue}{x} \cdot \frac{180^{\circ}}{\pi} \\
\end{split}
\end{equation}$$
Constants
ℯ (Euler's number)
$$\begin{equation}
\begin{split}
\mathrm{e}
&= \sum_{n = 0}^\infty \frac{1}{n!} \\
&= \lim_{n\to\infty} \left(1 + \frac{1}{n}\right)^n \\
&= \lim_{t \to 0} \left(1 + t\right)^{\frac{1}{t}}
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\mathrm{e}^x
&= 1 + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots \\
&= \sum_{n = 0}^\infty \frac{x^n}{n!} \\
&= \lim_{n\to\infty} \left(1 + \frac{x}{n}\right)^n
\end{split}
\end{equation}$$
Algebra
Properties
$$\begin{equation}
\begin{split}
a^m \cdot b^n &= a^{m+n}\\
\left(a^m\right)^n &= a^{m\cdot\,n} = \left(a^n\right)^m\\
\left(a\cdot\,b\right)^n &= a^n \cdot b^n\\
\left(\frac{a}{b}\right)^{-n} &= \left(\frac{b}{a}\right)^n\\
\frac{x^n}{y^n} &= \left(\frac{x}{y}\right)^n\\
x^{y^z} &= x^{\left(y ^ z\right)} \neq \left(x^y\right)^z
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
|x| &= \sqrt{x^2} \neq x
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\log_{\beta}(\alpha) &= \gamma\\
\beta^{\gamma} &= \alpha\\
\beta^{\log_{\beta}(N)} &= N\;\text{for all $N > 0$}\\
\log_{\beta}(\beta^x) &= x
\end{split}
\end{equation}$$
Trigonometry
Trigonometric Identities
Pythagorean Identities
$$\begin{equation}
\begin{split}
\cos^2(\theta) + \sin^2(\theta) = 1
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\sec^2(\theta) - \tan^2(\theta) &= 1 \\
\sec^2(\theta) &= 1 + \tan^2(\theta)
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\csc^2(\theta) - \cot^2(\theta) &= 1 \\
\csc^2(\theta) &= 1 + \cot^2(\theta)
\end{split}
\end{equation}$$
Sum and Difference Identities
$$
\begin{equation}
\begin{split}
\cos(\alpha - \beta) &= \cos(\alpha) \cdot \cos(\beta) + \sin(\alpha) \cdot \sin(\beta) \\
\cos(\alpha + \beta) &= \cos(\alpha) \cdot \cos(\beta) - \sin(\alpha) \cdot \sin(\beta) \\
&\\
\sin(\alpha - \beta) &= \sin(\alpha) \cdot \cos(\beta) - \cos(\alpha) \cdot \sin(\beta) \\
\sin(\alpha + \beta) &= \sin(\alpha) \cdot \cos(\beta) + \cos(\alpha) \cdot \sin(\beta) \\
&\\
\tan(\alpha + \beta) &= \frac{\tan(\alpha) + \tan(\beta)}{1 - \tan(\alpha) \cdot \tan(\beta)} \\
\tan(\alpha - \beta) &= \frac{\tan(\alpha) - \tan(\beta)}{1 + \tan(\alpha) \cdot \tan(\beta)}
\end{split}
\end{equation}
$$
Cofunction Identities
$$\begin{equation}
\begin{split}
\sin(\theta) = \cos(\frac{1}{4}\tau - \theta)
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\cos(\theta) = \sin(\frac{1}{4}\tau - \theta)
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\tan(\theta) = \cot(\frac{1}{4}\tau - \theta)
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\cot(\theta) = \tan(\frac{1}{4}\tau - \theta)
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\csc(\theta) = \sec(\frac{1}{4}\tau - \theta)
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\sec(\theta) = \csc(\frac{1}{4}\tau - \theta)
\end{split}
\end{equation}$$
Ratio Identities
$$
\begin{equation}
\begin{split}
\tan(90^\circ - x) & = \frac{\sin(90^\circ - x)}{\cos(90^\circ - x)} = \frac{\cos(x)}{\sin(x)} = \cot(x) \\
\\
\cot(90^\circ - x) & = \frac{\cos(90^\circ - x)}{\sin(90^\circ - x)} = \frac{\sin(x)}{\cos(x)} = \tan(x) \\
\end{split}
\end{equation}
$$
Double-Angle Identities
$$
\begin{equation}
\begin{split}
\sin(2\alpha) &= 2\sin(\alpha)\cos(\alpha) \\
\cos(2\alpha) &= \cos^2(\alpha) - \sin^2(\alpha) \\
&= 1 - 2\sin^2(\alpha) \\
&= 2\cos^2(\alpha) - 1 \\
&\\
\tan(2\alpha) &= \frac{2\tan(\alpha)}{1 - \tan^2(\alpha)}
\end{split}
\end{equation}
$$
Half-Angle Identities
$$
\begin{equation}
\begin{split}
\sin \frac{\alpha}{2} &= \pm \sqrt{\frac{1 - \cos(\alpha)}{2}} \\
\cos \frac{\alpha}{2} &= \pm \sqrt{\frac{1 + \cos(\alpha)}{2}} \\
\tan \frac{\alpha}{2} &= \pm \sqrt{\frac{1 - \cos(\alpha)}{1 + \cos(\alpha)}} \\
&= \frac{sin(\alpha)}{1 + \cos(\alpha)} \\
&= \frac{1 - \cos(\alpha)}{sin(\alpha)}
\end{split}
\end{equation}
$$
Power-Reducing Identities
$$
\begin{equation}
\begin{split}
\sin^2(\alpha) &= \frac{1 - \cos(2\alpha)}{2} \\
&\\
\cos^2(\alpha) &= \frac{1 + \cos(2\alpha)}{2} \\
&\\
\tan^2(\alpha) &= \frac{1 - \cos(2\alpha)}{1 + \cos(2\alpha)}
\end{split}
\end{equation}
$$
$$\begin{equation}
\begin{split}
\sin\alpha\cdot\cos\alpha &= \frac{1}{2}\sin(2\alpha)
\end{split}
\end{equation}$$
Product-to-Sum Identities
$$
\begin{equation}
\begin{split}
\sin(\alpha) \cdot \cos(\beta) &= \frac{1}{2} \Big[ \sin(\alpha + \beta) + \sin(\alpha - \beta) \Big] \\
\cos(\alpha) \cdot \sin(\beta) &= \frac{1}{2} \Big[ \sin(\alpha + \beta) - \sin(\alpha - \beta) \Big] \\
\cos(\alpha) \cdot \cos(\beta) &= \frac{1}{2} \Big[ \cos(\alpha + \beta) + \cos(\alpha - \beta) \Big] \\
\sin(\alpha) \cdot \sin(\beta) &= \frac{1}{2} \Big[ \cos(\alpha - \beta) - \cos(\alpha + \beta) \Big]
\end{split}
\end{equation}
$$
Sum-to-Product-Identities
$$
\begin{equation}
\begin{split}
\sin(x) + \sin(y) &= 2 \cdot \sin\left( \frac{x + y}{2} \right) \cdot \cos\left( \frac{x - y}{2} \right) \\
\cos(x) + \cos(y) &= 2 \cdot \cos\left( \frac{x + y}{2} \right) \cdot \cos\left( \frac{x - y}{2} \right) \\
\sin(x) - \sin(y) &= 2 \cdot \cos\left( \frac{x + y}{2} \right) \cdot \sin\left( \frac{x - y}{2} \right) \\
\cos(x) - \cos(y) &= -2 \sin \cos\left( \frac{x + y}{2} \right) \cdot \sin\left( \frac{x - y}{2} \right)
\end{split}
\end{equation}
$$
Trigonometric Equations
Euler's Formula
$$\begin{equation}
\begin{split}
e^{i x} &= \cos(x) + \mathrm{i}\sin(x)
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\mathrm{e}
&= \sum_{n = 0}^\infty \frac{1}{n!} \\
&= \lim_{n\to\infty} \left(1 + \frac{1}{n}\right)^n \\
&= \lim_{t \to 0} \left(1 + t\right)^{\frac{1}{t}}
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\mathrm{e}^x
&= 1 + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots \\
&= \sum_{n = 0}^\infty \frac{x^n}{n!} \\
&= \lim_{n\to\infty} \left(1 + \frac{x}{n}\right)^n
\end{split}
\end{equation}$$
Coordinate & Number Systems
$$\begin{equation}
\begin{split}
x &= r \cdot \cos\,\theta \\
y &= r \cdot \sin\,\theta \\
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
z &= x + \mathrm{i}y \\
&= r \left(\cos\, \theta + \mathrm{i}\sin\, \theta\right)\\
& = r\;\mathrm{cis}\; \theta \\
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
e^{i x} &= \cos\, x + \mathrm{i}\sin\, x \\
e ^{i x} &= r \left(\cos\, \theta + \mathrm{i}\sin\, \theta\right) \\
\left(\cos\, x + \mathrm{i}\sin\, x\right)^n &= \cos(n x) + \mathrm{i}\sin(n x) \\
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
r &= |z| = |x + \mathrm{i}y| = \sqrt{x^2 + y^2} \\
r^2 &= x^2 + y^2 \\
\tan \theta &= \frac{y}{x} \\
\theta &= \arctan\left(\frac{y}{x}\right)
\end{split}
\end{equation}$$
Polar Coordinate System
Given
$$\begin{equation}
\begin{split}
\tan \theta &= \frac{y}{x} \\
r^2 &= x^2 + y^2 \\
\end{split}
\end{equation}$$
Then
$$\begin{equation}
\begin{split}
x &= r \cdot \cos\,\theta \\
y &= r \cdot \sin\,\theta \\
\end{split}
\end{equation}$$
Properties
Given
$$\begin{equation}
\begin{split}
z_1 &= r_1\;\mathrm{cis}\;\theta_1 \\
z_2 &= r_1\;\mathrm{cis}\;\theta_1
\end{split}
\end{equation}$$
Then
$$\begin{equation}
\begin{split}
z_1 \cdot z_2 &= r_1 \cdot r_2 \;\mathrm{cis}\;\left(\theta_1 + \theta_2\right) \\
\frac{z_1}{z_2} &= \frac{r_1}{r_2} \;\mathrm{cis}\;\left(\theta_1 - \theta_2\right) \\
\end{split}
\end{equation}$$
De Moivre’s Theorem
$$\begin{equation}
\begin{split}
z^n &= r^n \;\mathrm{cis}\;\;n\theta
\end{split}
\end{equation}$$
De Moivre’s Theorem For Finding Roots
$$\begin{equation}
\begin{split}
\underbrace{w_k = r^{\frac{1}{n}}\;\mathrm{cis}\;\frac{\theta + \tau\cdot{k}}{n}}
_{\begin{split}\forall\; k &= 0,1,2\cdots,n-1\\ n &\geq 1\end{split}}
\end{split}
\end{equation}$$
Trigonometric form of a complex number
$$\begin{equation}
\begin{split}
z &= x + \mathrm{i}y \\
&= r \left(\cos\, \theta + \mathrm{i}\sin\, \theta\right)\\
& = r\;\mathrm{cis}\;\theta \\
\end{split}
\end{equation}$$
Vectors
Quick Facts
-
Two vectors are equal if they share the same magnitude and direction.
Initial points don't matter. -
You can define a vector with two points.
-
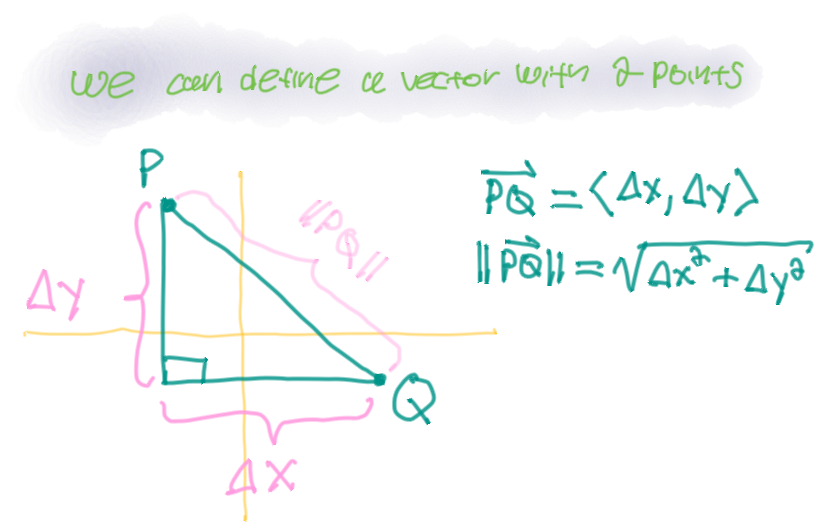
Do not divide vectors!
- \(\vec{v} \cdot \vec{v} = ||\vec{v}||^2 \implies \text{constant}\)
- \(\vec{v} \cdot \left(\vec{v}\right)^\prime = 0\)
Vector Operations
Dot Product
$$\begin{equation}
\begin{split}
\vec{a}\cdot\vec{b}
&= \begin{bmatrix} a_1 \\ a_2 \\ a_3 \end{bmatrix}
\cdot
\begin{bmatrix} b_1 \\ b_2 \\ b_3 \end{bmatrix}
= a_1b_1 + a_2b_2 + a_3b_3\\\\
\vec{a}\cdot\vec{b}
&= \begin{bmatrix} a_1 \\ a_2 \end{bmatrix}
\cdot
\begin{bmatrix} b_1 \\ b_2 \end{bmatrix}
= a_1b_1 + a_2b_2
\end{split}
\end{equation}$$
Cross Product
$$\begin{equation}
\begin{split}
\vec{a}\times\vec{b}
&=
\begin{bmatrix} a_1 & a_2 & a_3 \end{bmatrix}\times\begin{bmatrix} b_1 & b_2 & b_3 \end{bmatrix}\\
&=
\mathrm{det}
\begin{pmatrix}
\mathrm{\hat{i}} & \mathrm{\hat{j}} & \mathrm{\hat{k}}\\
a_1 & a_2 & a_3\\
b_1 & b_2 & b_3
\end{pmatrix}\\
&=
\mathrm{\hat{i}}
\begin{vmatrix}
e & f\\
h & i
\end{vmatrix}
-
\mathrm{\hat{j}}
\begin{vmatrix}
d & f\\
g & i
\end{vmatrix}
+
\mathrm{\hat{k}}
\begin{vmatrix}
d & e\\
g & h
\end{vmatrix}\\
&= \mathrm{\hat{i}}\left(e i - f h\right)
- \mathrm{\hat{j}}\left(d i - f g\right)
+ \mathrm{\hat{k}}\left(d h - e g\right)\\
&=
\begin{bmatrix}
e i - f h &
d i - f g &
d h - e g
\end{bmatrix}\\
&= \vec{c}
\end{split}
\end{equation}$$
Length of a Vector
$$\begin{equation}
\begin{split}
|a| &= \sqrt{(a_1)^2 + (a_2)^2} \\
|a| &= \sqrt{(a_1)^2 + (a_2)^2 + (a_3)^2}
\end{split}
\end{equation}$$
Definition of Vector Addition
If \(\vec{u}\) and \(\vec{v}\) are positioned so the initial point of \(\vec{v}\) is at the terminal point of \(\vec{u}\), then the sum \(\vec{u} + \vec{v}\) is the vector from the initial point of \(\vec{u}\) to the terminal point of \(\vec{v}\).
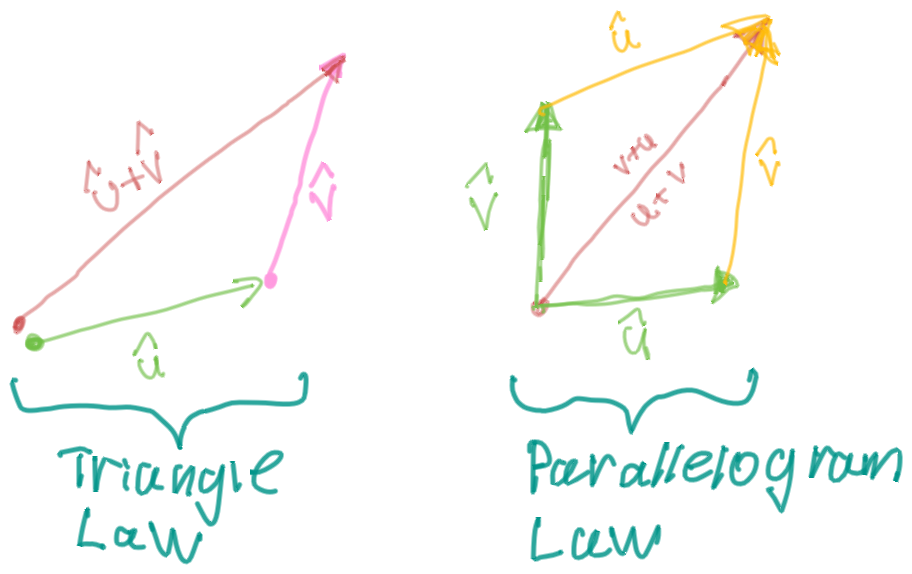
Given some vectors \(\vec{u}\) and \(\vec{v}\), the vector \(\vec{u} - \vec{v}\) is the vector that points from the head of \(\vec{v}\) to the head of \(\vec{u}\)
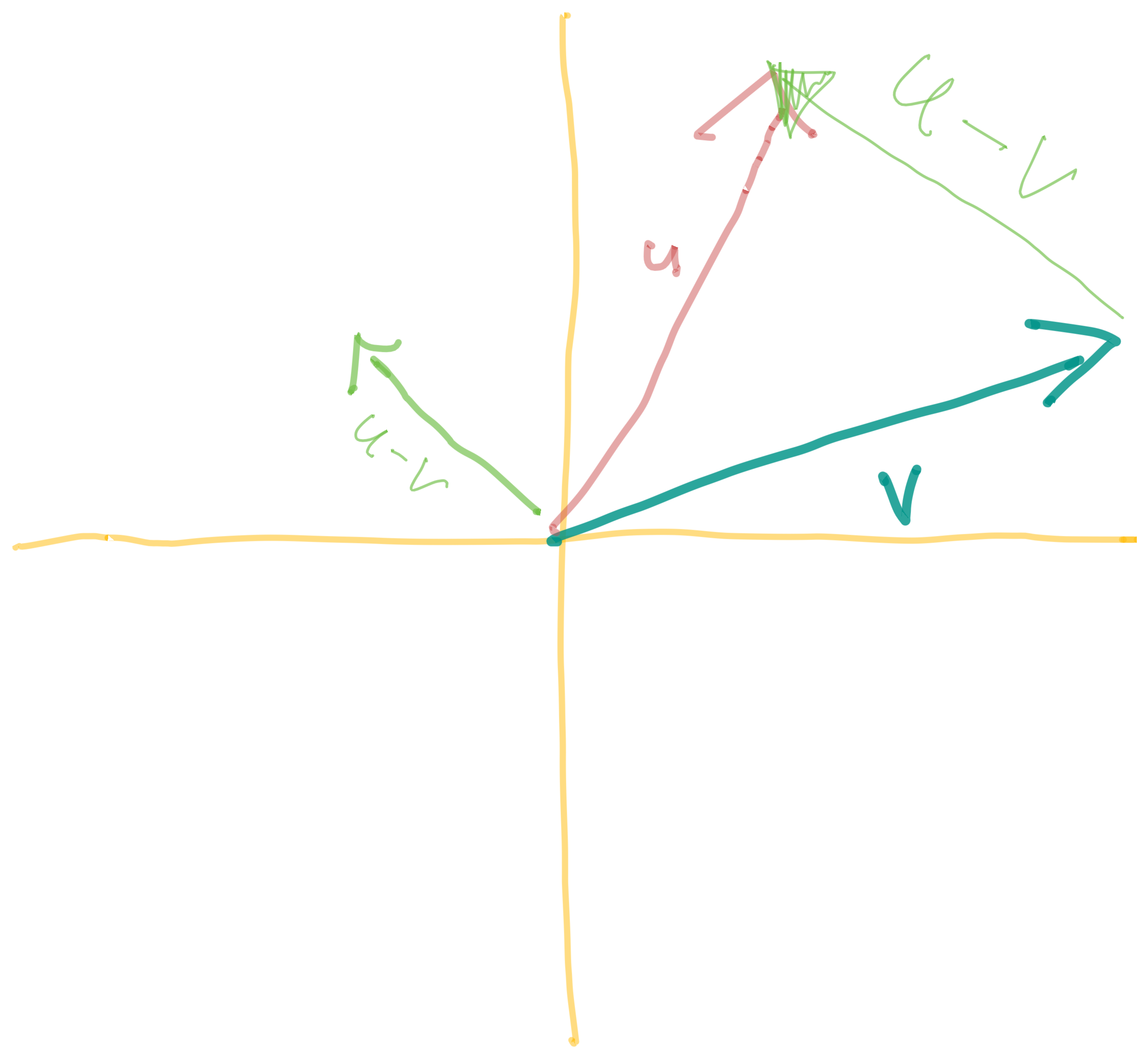
Standard Basis Vectors
$$\begin{equation}
\begin{split}
\mathrm{\hat{i}} &= \begin{bmatrix} 1 & 0 & 0 \end{bmatrix}\\
\mathrm{\hat{j}} &= \begin{bmatrix} 0 & 1 & 0 \end{bmatrix}\\
\mathrm{\hat{k}} &= \begin{bmatrix} 0 & 0 & 1 \end{bmatrix}
\end{split}
\end{equation}$$
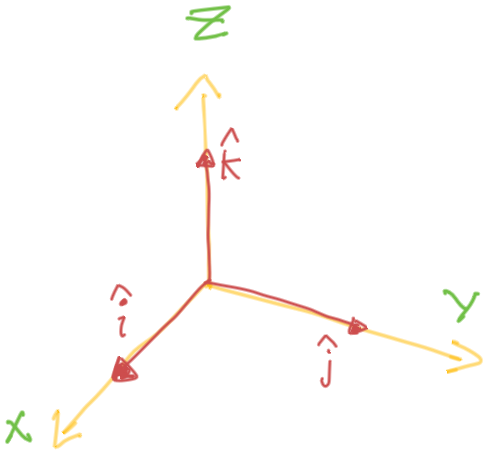
Orthogonal
Two vectors are orthogonal if and only if
$$\begin{equation}
\begin{split}
\vec{a}\cdot\vec{b} = 0
\end{split}
\end{equation}$$
The Unit Vector
$$\begin{equation}
\begin{split}
\hat{u} &= \frac{\vec{a}}{|\vec{a}|}
\end{split}
\end{equation}$$
If \(\theta\) is the angle between the vectors \(\vec{a}\) and \(\vec{b}\), then
$$\begin{equation}
\begin{split}
\vec{a} \cdot \vec{a} = |\vec{a}| \cdot |\vec{a}| \cos\theta
\end{split}
\end{equation}$$
If \(\theta\) is the angle between the nonzero vectors \(\vec{a}\) and \(\vec{b}\), then
$$\begin{equation}
\begin{split}
\cos\theta = \frac
{\vec{a}\cdot\vec{b}}
{|\vec{a}| |\vec{b}|}
\end{split}
\end{equation}$$
Two nonzero vectors \(\vec{a}\) and \(\vec{b}\) are parallel if and only if
$$\begin{equation}
\begin{split}
\vec{a}\times\vec{b} = 0
\end{split}
\end{equation}$$
Properties of the Dot Product
$$\begin{equation}
\begin{split}
\vec{a} \cdot \vec{a} = |\vec{a}|^2
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\vec{a} \cdot \left(\vec{b} + \vec{c}\right) = \vec{a}\vec{b} + \vec{a}\vec{c}
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\left(c \cdot \vec{a}\right) \cdot \vec{b} = c\left(\vec{a} \cdot \vec{b}\right)
\end{split}
\end{equation}$$
Direction Cosines & Direction Angles of a Vector
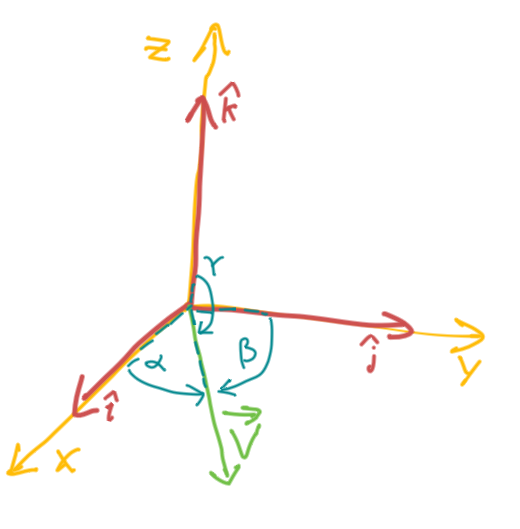
Where
$$\begin{equation}
\begin{split}
\vec{v} &= \begin{bmatrix} v_x & v_y & v_z \end{bmatrix}
\;\;\;\;
||\vec{v}|| &= \sqrt{(v_x)^2 + (v_y)^2 + (v_z)^2}
\end{split}
\end{equation}$$
Direction Cosines
$$\begin{equation}
\begin{split}
\cos\alpha &= \frac{v_x}{||\vec{v}||}\\
\cos\beta &= \frac{v_y}{||\vec{v}||}\\
\cos\gamma &= \frac{v_z}{||\vec{v}||}
\end{split}
\end{equation}$$
Direction Angles
$$\begin{equation}
\begin{split}
\alpha &= \arccos \left(\frac{v_x}{||\vec{v}||}\right)\\
\beta &= \arccos \left(\frac{v_y}{||\vec{v}||}\right)\\
\gamma &= \arccos \left(\frac{v_z}{||\vec{v}||}\right)
\end{split}
\end{equation}$$
Theorem
$$\begin{equation}
\begin{split}
\cos^2\alpha + \cos^2\beta + \cos^2\gamma = 1
\end{split}
\end{equation}$$
Proof
$$\begin{equation}
\begin{split}
\vec{v} &= \hat{i}\cos\alpha + \hat{k}\cos\beta + \hat{k}\cos\gamma\\
||\vec{v}|| &= || \hat{i}\cos\alpha + \hat{k}\cos\beta + \hat{k}\cos\gamma|| = 1
\end{split}
\end{equation}$$
Given
$$\begin{equation}
\begin{split}
\sqrt{\cos^2\alpha + \cos^2\beta + \cos^2\gamma} &= 1\\
\sqrt{\cos^2\alpha + \cos^2\beta + \cos^2\gamma}^2 &= 1^2\\
\cos^2\alpha + \cos^2\beta + \cos^2\gamma &= 1
\end{split}
\end{equation}$$
Therefore
$$\begin{equation}
\begin{split}
\cos^2\alpha + \cos^2\beta + \cos^2\gamma = 1\\
\end{split}
\end{equation}$$
Vector Relations
Parallel Vectors
- When two vectors are parallel; they never intersect (duh).
Given some vectors
$$\begin{equation}
\begin{split}
\vec{a} &= \begin{bmatrix} a_x & a_y & a_z \end{bmatrix}\\
\vec{b} &= \begin{bmatrix} b_x & b_y & b_z \end{bmatrix}
\end{split}
\end{equation}$$
The vectors \(\vec{a}\) and \(\vec{b}\) are parallel if and only if they are scalar multiples of one another.
$$\begin{equation}
\begin{split}
\vec{a} &= k\;\vec{b} \;\;\;\;\forall k \neq 0
\end{split}
\end{equation}$$
Alternatively
$$\begin{equation}
\begin{split}
\frac{a_x}{b_x} = \frac{a_y}{b_y} = \frac{a_z}{b_z}
\end{split}
\end{equation}$$
Orthogonal Vectors
- When two vectors are orthogonal; they meet at right angles.
Given some vectors
$$\begin{equation}
\begin{split}
\vec{a} &= \begin{bmatrix} a_x & a_y & a_z \end{bmatrix}\\
\vec{b} &= \begin{bmatrix} b_x & b_y & b_z \end{bmatrix}
\end{split}
\end{equation}$$
Two vectors are orthogonal if and only if
$$\begin{equation}
\begin{split}
\vec{a}\times\vec{b} = 0
\end{split}
\end{equation}$$
Reparameterization of the position vector \(\vec{v}(t)\) in terms of length \(S(t)\)
-
We can parametrize a curve with respect to arc length; because arc length arises naturally from the shape of the curve and does not depend on any coordinate system.
The Arc Length Function
Given
$$\begin{equation}
\begin{split}
\vec{v}
&= \begin{bmatrix} x & y & z \end{bmatrix}
= \begin{bmatrix} f(t) & g(t) & h(t) \end{bmatrix}
\end{split}
\end{equation}$$
We can redefine \(\vec{v}\) in terms of arc length between two endpoints
$$
\newcommand{\Long}{
\int_a^t \sqrt{
\left(f^\prime(u)\right)^2
\left(g^\prime(u)\right)^2
\left(h^\prime(u)\right)^2
}
}
\newcommand{\AltLong}{
\int_a^t \sqrt{
\left(\frac{\mathrm{d}x}{\mathrm{d}u}\right)^2
\left(\frac{\mathrm{d}y}{\mathrm{d}u}\right)^2
\left(\frac{\mathrm{d}z}{\mathrm{d}u}\right)^2
}
}
\newcommand{\short}{
\int_a^t ||\left(v^\prime(u)\right)||
}
\begin{equation}
\begin{split}
S(t)
&= \Long\\
&= \AltLong\\
&= \short
\end{split}
\end{equation}
$$
That is, \(S(t)\) is the length of the curve (\(C\)) between \(r(a)\) and \(r(b)\).
Furthermore from the adjacent definition; we can simply the above to
$$\begin{equation}
\begin{split}
S(t) = \int_a^t \frac{\mathrm{d}S}{\mathrm{d}t}
\end{split}
\end{equation}$$
The Arc Length Function
$$\begin{equation}
\begin{split}
\frac{\mathrm{d}S}{\mathrm{d}t} \equiv || v^\prime(t) ||
\end{split}
\end{equation}$$
That is
$$
\newcommand{\Long}{
\sqrt{
\left(f^\prime(u)\right)^2
\left(g^\prime(u)\right)^2
\left(h^\prime(u)\right)^2
}
}
\newcommand{\AltLong}{
\sqrt{
\left(\frac{\mathrm{d}x}{\mathrm{d}u}\right)^2
\left(\frac{\mathrm{d}y}{\mathrm{d}u}\right)^2
\left(\frac{\mathrm{d}z}{\mathrm{d}u}\right)^2
}
}
\newcommand{\short}{
||\left(v^\prime(u)\right)||
}
\begin{equation}
\begin{split}
\frac{\mathrm{d}S}{\mathrm{d}t}
&= \Long\\
&= \AltLong\\
&= \short
\end{split}
\end{equation}
$$
Vectors Derived From Some Curve Defined by \(\vec{v}\)
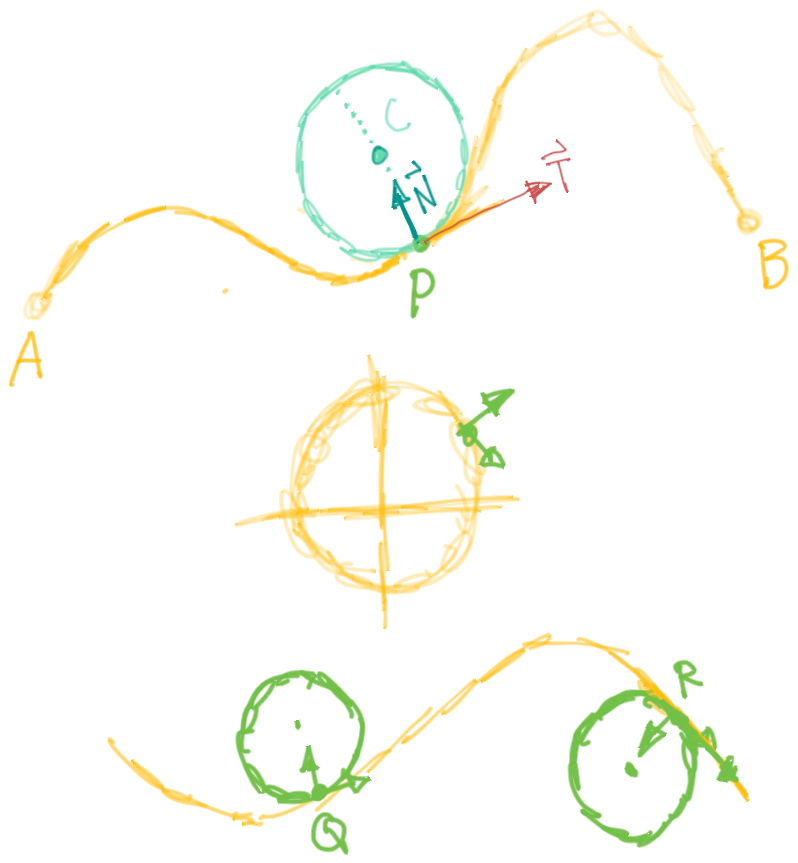
The Unit Vector
$$\begin{equation}
\begin{split}
\hat{U} \equiv \frac{\vec{v}}{||\vec{v}||}
\end{split}
\end{equation}$$
The Unit Tangent Vector
$$\begin{equation}
\begin{split}
\vec{T}
&\equiv \frac
{v^\prime(t)}
{||v^\prime(t)||}
&\equiv \frac
{\mathrm{d}v}
{\mathrm{d}S}
\end{split}
\end{equation}$$
The Unit Normal Vector
$$\begin{equation}
\begin{split}
\vec{N} \equiv \frac
{T^\prime}
{||T^\prime||}
\end{split}
\end{equation}$$
The Binormal Vector
$$\begin{equation}
\begin{split}
\vec{B} \equiv \vec{T}\times\vec{N}
\end{split}
\end{equation}$$
-
Therefore, the binormal vector is orthogonal to both the tangent vector and the normal vector.
-
The plane determined by the normal and binormal vectors N and B at a point P on a curve C is called the normal plane of C at P.
-
The plane determined by the vectors T and N is called the osculating plane of C at P. The name comes from the Latin osculum, meaning “kiss.” It is the plane that comes closest to containing the part of the curve near P. (For a plane curve, the osculating plane is simply the plane that contains the curve.)
Kappa - Curvature of a Vector
$$\begin{equation}
\begin{split}
\kappa
&\equiv \left|\frac{\mathrm{d}T}{\mathrm{d}S}\right|
&\equiv \frac
{\left| T^\prime \right|}
{\left| r^\prime \right|}
&\equiv \frac
{\left| r^\prime \times r^{\prime\prime} \right|}
{\left| r^\prime \right|^3}
\end{split}
\end{equation}$$
Tangential & Normal Components of the Acceleration Vector of the Curve
When we study the motion of a particle, it is often useful to resolve the acceleration into two components, one in the direction of the tangent and the other in the direction of the normal.
$$\begin{equation}
\begin{split}
a_{\vec{T}}
&= \frac{\mathrm{d}}{\mathrm{d}t} \left|\vec{v}\right|
= \frac{r^\prime \cdot r^{\prime\prime}}{|r^\prime|}\\
a_{\vec{N}}
&= \kappa \left|\vec{v}\right|^2
= \frac{\left|r^\prime \times r^{\prime\prime}\right|}{|r^\prime|}\\
\vec{a} &= a_{\vec{T}} \vec{T} + a_{\vec{N}} \vec{N}
\end{split}
\end{equation}$$
Specifically
$$\begin{equation}
\begin{split}
\left.\begin{aligned}
a_{\vec{T}}\\
a_{\vec{N}}
\end{aligned}\right\} \text{Tangential & Normal Components of $\vec{a}$}
\end{split}
\end{equation}$$
Vector Calculus
The Position Vector \(\vec{r}(t)\)
(Original Function)
The Velocity Vector \(\vec{v}(t)\)
(First Derivative)
- The velocity vector is also the tangent vector and points in the direction of the tangent line.
- The speed of the particle at time t is the magnitude of the velocity vector, that is,
$$\begin{equation} \begin{split} \underbrace{|\vec{v}(t)| = |(\vec{r})^\prime(t)| = \frac{\mathrm{d}s}{\mathrm{d}t}} _{\text{rate of change of distance with respect to time}} \end{split} \end{equation}$$
The Acceleration Vector \(\vec{a}(t)\)
(Second Derivative)
Matrices
Reference
The Determinant of A Matrix
$$\begin{equation}
\begin{split}
|A| &=
\begin{vmatrix}
a & b\\
c & d
\end{vmatrix} =
ad - bc\\\\
|A| &=
\begin{vmatrix}
a & b & c\\
d & e & f\\
g & h & i
\end{vmatrix}\\ &=
a
\begin{vmatrix}
e & f\\
h & i
\end{vmatrix}
-
b
\begin{vmatrix}
d & f\\
g & i
\end{vmatrix}
+
c
\begin{vmatrix}
d & e\\
g & h
\end{vmatrix}
\end{split}
\end{equation}$$
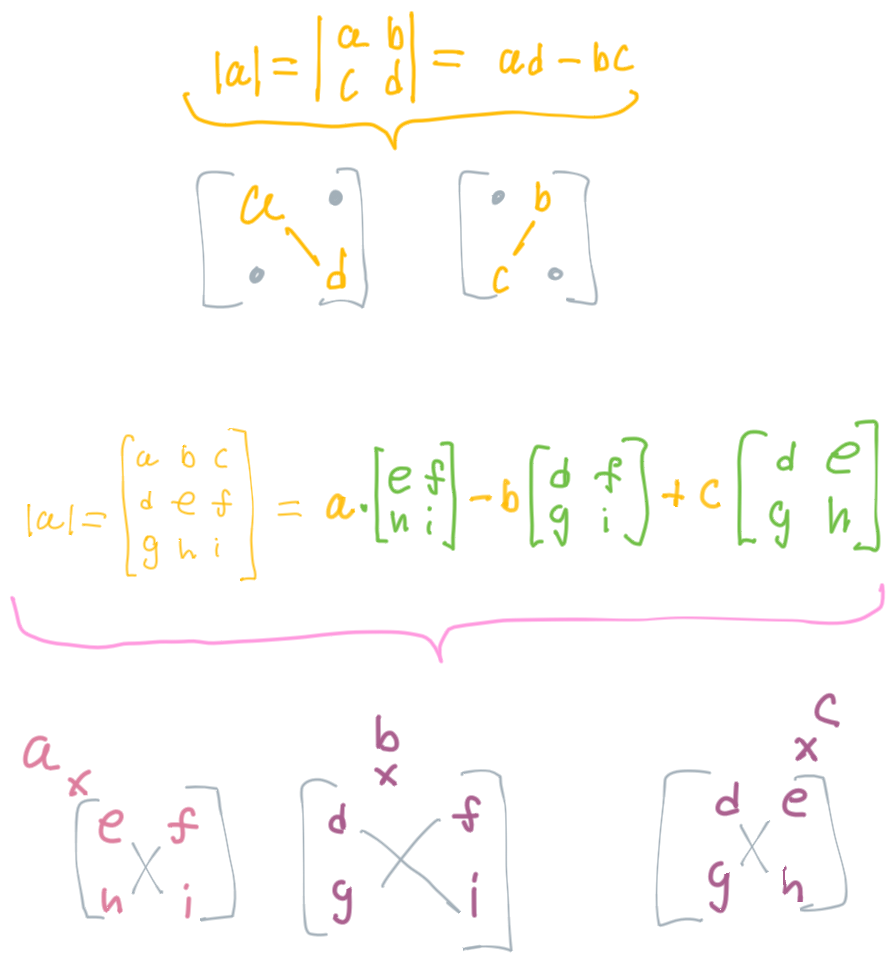
Only works for square matrices.
The Cross Product
$$\begin{equation}
\begin{split}
\vec{a}\times\vec{b}
&=
\begin{bmatrix} a_1 & a_2 & a_3 \end{bmatrix}\times\begin{bmatrix} b_1 & b_2 & b_3 \end{bmatrix}\\
&=
\mathrm{det}
\begin{pmatrix}
\mathrm{\hat{i}} & \mathrm{\hat{j}} & \mathrm{\hat{k}}\\
a_1 & a_2 & a_3\\
b_1 & b_2 & b_3
\end{pmatrix}\\
&=
\mathrm{\hat{i}}
\begin{vmatrix}
e & f\\
h & i
\end{vmatrix}
-
\mathrm{\hat{j}}
\begin{vmatrix}
d & f\\
g & i
\end{vmatrix}
+
\mathrm{\hat{k}}
\begin{vmatrix}
d & e\\
g & h
\end{vmatrix}\\
&= \mathrm{\hat{i}}\left(e i - f h\right)
- \mathrm{\hat{j}}\left(d i - f g\right)
+ \mathrm{\hat{k}}\left(d h - e g\right)\\
&=
\begin{bmatrix}
e i - f h &
d i - f g &
d h - e g
\end{bmatrix}\\
&= \vec{c}
\end{split}
\end{equation}$$
Geometry
Definition of a Line
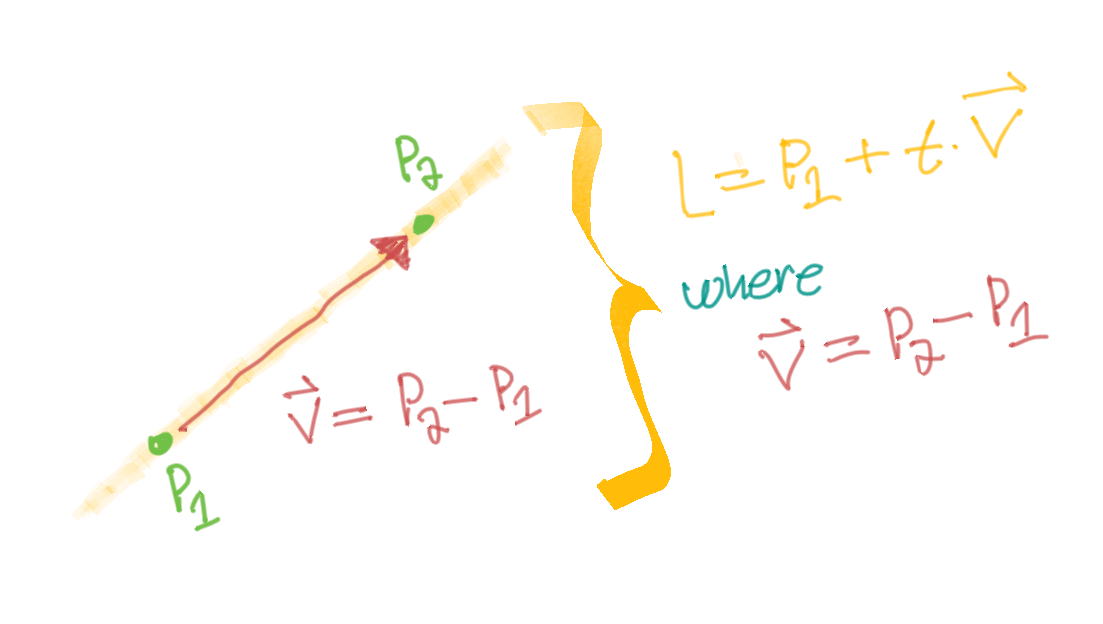
Vector Equation of a Line
Given
$$\begin{equation}
\begin{split}
\colorB{P_1} &= \begin{bmatrix} \colorB{x_1} & \colorB{y_1} & \colorB{z_1} \end{bmatrix}\\
\colorC{P_2} &= \begin{bmatrix} \colorC{x_2} & \colorC{y_2} & \colorC{z_2} \end{bmatrix}\\
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\colorB{P_1} &= \begin{bmatrix} \colorB{x_1} & \colorB{y_1} & \colorB{z_1} \end{bmatrix}\\
\colorC{P_2} &= \begin{bmatrix} \colorC{x_2} & \colorC{y_2} & \colorC{z_2} \end{bmatrix}\\
\end{split}
\end{equation}$$
We can define a vector between \(\colorB{P_1}\) and \(\colorC{P_2}\)
$$\begin{equation}
\begin{split}
\colorA{\overrightarrow{\Delta\mathsf{v}}} &=
\begin{bmatrix} \colorC{x_2} \\ \colorC{y_2} \\ \colorC{z_2} \end{bmatrix} -
\begin{bmatrix} \colorB{x_1} \\ \colorB{y_1} \\ \colorB{z_1} \end{bmatrix} =
\begin{bmatrix} \colorC{x_2}-\colorB{x_1} \\ \colorC{y_2}-\colorB{y_1} \\ \colorC{z_2}-\colorB{z_1} \end{bmatrix} =
\begin{bmatrix} \colorA{\Delta_x} \\ \colorA{\Delta_y} \\ \colorA{\Delta_z} \end{bmatrix}
\end{split}
\end{equation}$$
Therefore
The equation of a line in 3D space or \(\mathbb{R}^3\) can be defined VIA the following options
$$\begin{equation}
\begin{split}
L &= \colorB{P_1} + t\cdot\colorA{\overrightarrow{\Delta\mathsf{v}}} \\
\begin{bmatrix} x \\ y \\ z \end{bmatrix} &=
\begin{bmatrix} \colorB{x_1} \\ \colorB{y_1} \\ \colorB{z_1} \end{bmatrix} +
t\begin{bmatrix} \colorA{\Delta_x} \\ \colorA{\Delta_y} \\ \colorA{\Delta_z} \end{bmatrix} =
\begin{bmatrix} \colorB{x_1} \\ \colorB{y_1} \\ \colorB{z_1} \end{bmatrix} +
\begin{bmatrix} t\;\colorA{\Delta_x} \\ t\;\colorA{\Delta_y} \\ t\;\colorA{\Delta_z} \end{bmatrix} \\
&=
\begin{bmatrix} \colorB{x_1} + t\;\colorA{\Delta_x} \\ \colorB{y_1} + t\;\colorA{\Delta_y} \\ \colorB{z_1} + t\;\colorA{\Delta_z} \end{bmatrix}\\
&=
\begin{bmatrix} \colorB{x_1} + t(\colorC{x_2}-\colorB{x_1}) \\ \colorC{x_2} + t(\colorC{x_2}-\colorB{x_1}) \\ x_3 + t(\colorC{x_2}-\colorB{x_1}) \end{bmatrix}
\end{split}
\end{equation}$$
That is
$$\begin{equation}
\begin{split}
L &= \colorB{P_1} + t\cdot\colorA{\overrightarrow{\Delta\mathsf{v}}}\\
\begin{bmatrix} x \\ y \\ z \end{bmatrix} &=
\begin{bmatrix} \colorB{x_1} + t\;\colorA{\Delta_x} \\ \colorB{y_1} + t\;\colorA{\Delta_y} \\ \colorB{z_1} + t\;\colorA{\Delta_z} \end{bmatrix}
= \begin{bmatrix} \colorB{x_1} + t(\colorC{x_2}-\colorB{x_1}) \\ \colorB{y_1} + t(\colorC{y_2}-\colorB{y_1}) \\ \colorB{z_1} + t(\colorC{z_2}-\colorB{z_1}) \end{bmatrix}
\end{split}
\end{equation}$$
Parametric Equation of a Line
$$\begin{equation}
\begin{split}
\underbrace{\begin{split}
x &= \colorB{x_1} + t(\colorC{x_2}-\colorB{x_1}) = \colorB{x_1} + t\;\colorA{\Delta_x}\\
y &= \colorB{x_1} + t(\colorC{y_2}-\colorB{y_1}) = \colorB{y_1} + t\;\colorA{\Delta_y}\\
z &= \colorB{x_1} + t(\colorC{z_2}-\colorB{z_1}) = \colorB{z_1} + t\;\colorA{\Delta_z}
\end{split}}_{
r \;=\; r_0 \;+\; a \;=\; r_0 \;+\; t\,v
}
\end{split}
\end{equation}$$
Essentially
$$\begin{equation}
\begin{split}
L &= \colorB{P_1} + t\cdot\colorA{\overrightarrow{\Delta\mathsf{v}}}\;\;\forall t\in\mathbb{R}
\end{split}
\end{equation}$$
That is, \(t\) is the scaling factor. In a way, it's like it's a function of \(t\), but also similar to the slope (\(m\)) in \(y = mx + b\), except \(m\) (i.e. \(t\)) is parameterized.
Sometimes this will be (confusingly) denoted as
$$\begin{equation}
\begin{split}
\vec{r} &= \vec{r_0} + \vec{a} = \vec{r_0} + t\vec{v}\\
\end{split}
\end{equation}$$
Symmetric Equation of a Line
$$\begin{equation}
\begin{split}
t &= \frac{x - \colorB{x_1}}{\colorC{x_2}-\colorB{x_1}} = \frac{x - \colorB{x_1}}{\colorA{\Delta_x}}\\
t &= \frac{y - \colorB{y_1}}{\colorC{y_2}-\colorB{y_1}} = \frac{y - \colorB{y_1}}{\colorA{\Delta_y}}\\
t &= \frac{z - \colorB{z_1}}{\colorC{z_2}-\colorB{z_1}} = \frac{z - \colorB{z_1}}{\colorA{\Delta_z}}
\end{split}
\end{equation}$$
Therefore
$$\begin{equation}
\begin{split}
\frac{x - \colorB{x_1}}{\colorA{\Delta_x}}
&= \frac{y - \colorB{y_1}}{\colorA{\Delta_y}}
= \frac{z - \colorB{z_1}}{\colorA{\Delta_z}}
\\\\
\frac{x - \colorB{x_1}}{\colorC{x_2}-\colorB{x_1}}
&= \frac{y - \colorB{y_1}}{\colorC{y_2}-\colorB{y_1}}
= \frac{z - \colorB{z_1}}{\colorC{z_2}-\colorB{z_1}}
\end{split}
\end{equation}$$
Rationale
We rewrite \(r = r_0 + a = r_0 + t v\) in terms of \(t\).
That is
$$\begin{equation}
\begin{split}
x &= \colorB{x_1} + t(\colorC{x_2}-\colorB{x_1}) = \colorB{x_1} + t\;\colorA{\Delta_x}\\
t\;\colorA{\Delta_x} &= x - \colorB{x_1} = t(\colorC{x_2}-\colorB{x_1})\\
t &= \frac{x - \colorB{x_1}}{\colorC{x_2}-\colorB{x_1}} = \frac{x - \colorB{x_1}}{\colorA{\Delta_x}} \\\\
y &= \colorB{y_1} + t(\colorC{y_2}-\colorB{y_1}) = \colorB{y_1} + t\;\colorA{\Delta_y}\\
t\;\colorA{\Delta_y} &= y - \colorB{y_1} = t(\colorC{y_2}-\colorB{y_1})\\
t &= \frac{y - \colorB{y_1}}{\colorC{y_2}-\colorB{y_1}} = \frac{y - \colorB{y_1}}{\colorA{\Delta_y}} \\\\
z &= \colorB{z_1} + t(\colorC{z_2}-\colorB{z_1}) = \colorB{z_1} + t\;\colorA{\Delta_z}\\
t\;\colorA{\Delta_z} &= z - \colorB{z_1} = t(\colorC{z_2}-\colorB{z_1}) \\
t &= \frac{z - \colorB{z_1}}{\colorC{z_2}-\colorB{z_1}} = \frac{z - \colorB{z_1}}{\colorA{\Delta_z}}
\end{split}
\end{equation}$$
Parameterizations of a curve
- Parametrized curve
- A curve in the plane is said to be parameterized if the set of coordinates on the curve, (x,y), are represented as functions of a variable t.
- A parametrized Curve is a path in the xy-plane traced out by the point \(\left(x(t), y(t)\right)\) as the parameter \(t\) ranges over an interval \(I\).
- A parametrized Curve is a path in the xyz-plane traced out by the point \(\left(x(t), y(t), z(t)\right)\) as the parameter \(t\) ranges over an interval \(I\).
Curvature Properties
Length of a Curve
$$
\newcommand{\Long}{
\int_a^b \sqrt{
\left(f^\prime(t)\right)^2
\left(g^\prime(t)\right)^2
\left(h^\prime(t)\right)^2
}
}
\newcommand{\AltLong}{
\int_a^b \sqrt{
\left(\frac{\mathrm{d}x}{\mathrm{d}t}\right)^2
\left(\frac{\mathrm{d}y}{\mathrm{d}t}\right)^2
\left(\frac{\mathrm{d}z}{\mathrm{d}t}\right)^2
}
}
\newcommand{\short}{
\int_a^b ||\left(r^\prime(t)\right)||
}
\begin{equation}
\begin{split}
L &= \Long\\
&= \AltLong\\
&= \short\\
&\implies \text{some constant}
\end{split}
\end{equation}
$$
The Arc Length Function
Suppose
-
Given some curve \(C\) defined by some vector \(\vec{r}\) in \(\mathbb{R}^3\)
-
where \(r^\prime\) is continuous and \(C\) is traversed exactly once as \(t\) increases from \(a\) to \(b\)
We can define it's arc length function VIA
$$
\newcommand{\Long}{
\int_a^t \sqrt{
\left(f^\prime(u)\right)^2
\left(g^\prime(u)\right)^2
\left(h^\prime(u)\right)^2
}
}
\newcommand{\AltLong}{
\int_a^t \sqrt{
\left(\frac{\mathrm{d}x}{\mathrm{d}u}\right)^2
\left(\frac{\mathrm{d}y}{\mathrm{d}u}\right)^2
\left(\frac{\mathrm{d}z}{\mathrm{d}u}\right)^2
}
}
\newcommand{\short}{
\int_a^t ||\left(r^\prime(u)\right)||
}
\begin{equation}
\begin{split}
S(t)
&= \Long\\
&= \AltLong\\
&= \short
\end{split}
\end{equation}
$$
Limits
L’Hospital’s Rule
$$\begin{equation}
\begin{split}
\lim_{x\to{a}}\frac{f(x)}{g(x)} &= \lim_{x\to{a}}\frac{f^\prime(x)}{g^\prime(x)}\\
\text{if}\;\lim_{x\to{a}}\frac{f(x)}{g(x)} = \frac{0}{0}
\;&\text{or}\;\lim_{x\to{a}}\frac{f(x)}{g(x)} = \frac{\infty}{\infty}
\end{split}
\end{equation}$$
In other words, if L’Hospital’s Rule applies to indeterminate forms.
Limit Laws
$$\begin{equation}
\begin{split}
\lim_{x \to a} \Big[ f(x) + g(x) \Big] &= \lim_{x \to a} f(x) + \lim_{x \to a} g(x)
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\lim_{x \to a} \Big[ f(x) - g(x) \Big] &= \lim_{x \to a} f(x) - \lim_{x \to a} g(x)
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\lim_{x \to a} \Big[ c \cdot f(x) \Big] &= c \cdot \lim_{x \to a} f(x)
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\lim_{x \to a} \Big[ f(x) \cdot g(x) \Big] &= \lim_{x \to a} f(x) \cdot \lim_{x \to a} g(x)
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\lim_{x \to a} \frac{f(x)}{g(x)} &= \frac{\lim_{x \to a} f(x)}{\lim_{x \to a}g(x)} \; \text{if} \lim_{x \to a}g(x) \neq 0
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\lim_{x \to a} \Big[ f(x) \Big]^n = \Big[ \lim_{x \to a} f(x) \Big]^n\;\text{if}\;n\in\mathbb{Z}^+
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\underbrace{\lim_{x \to a} \sqrt[n]{f(x)} = \sqrt[n]{\lim_{x \to a} f(x)}\;\text{if}\;n\in\mathbb{Z}^+}_{\text{if $n$ is even we assume $\lim_{x \to a} f(x) > 0$}}
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\lim_{x\to{c}}\, \left(f \circ g\right)(x) &= f\left(\lim_{x\to{c}}\, g(x)\right)
\end{split}
\end{equation}$$
Limit Formulas
$$\begin{equation}
\begin{split}
\lim_{x\to\infty} \frac{1}{x^r} &= 0\;,\;\forall r > 0
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\lim_{x\to\infty} \frac{x^n}{!n} &= 0\;,\;\forall n \in \mathbb{R}
\end{split}
\end{equation}$$
Growth Rates
- Factorial functions grow faster than exponential functions.
- Exponential functions grow faster than polynomials.
Calculus
Derivative Tables
$$\begin{equation}
\begin{split}
\delta\sin(x) &= \cos(x) \\
\delta\csc(x) &= -\cot(x) \cdot \csc(x)
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\delta\cos(x) &= -\sin(x) \\
\delta\sec(x) &= \tan(x) \cdot \sec(x)
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\delta\tan(x) &= \sec^2(x) \\
\delta\cot(x) &= -\csc^2(x)
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\delta\sin^{-1}(x) &= \frac{1}{\sqrt{1 - x^2}}
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\delta\cos^{-1}(x) &= -\frac{1}{\sqrt{1 - x^2}}
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\delta\tan^{-1}(x) &= \frac{1}{1 + x^2}
\end{split}
\end{equation}$$
Integration Tables
$$\begin{equation}
\begin{split}
\int\sin(x)\;\mathrm{d}x &= -\cos x \\
\int\csc^2(x)\;\mathrm{d}x &= -\cot x \\
\int\csc(x)\cdot\cot(x)\;\mathrm{d}x &= -\csc x \\
\int\csc(x)\;\mathrm{d}x &= \ln\left|\csc x - \cot x\right| \\
\int\sinh(x)\;\mathrm{d}x &= \cosh(x) \\
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\int\cos(x)\;\mathrm{d}x &= \sin x \\
\int\sec^2(x)\;\mathrm{d}x &= \tan x \\
\int\sec(x)\cdot\tan(x)\;\mathrm{d}x &= \sec x \\
\int\sec(x)\;\mathrm{d}x &= \ln\left|\sec x + \tan x\right| \\
\int\cosh(x)\;\mathrm{d}x &= \sinh(x) \\
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\int\tan(x)\;\mathrm{d}x &= \ln| \sec x | \\
\int\cot(x)\;\mathrm{d}x &= \ln| \sin x | \\
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\int b^x\;\mathrm{d}x &= \frac{b^x}{\ln(b)}
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\int\frac{1}{x^2 + a^2}\;\mathrm{d}x &= \frac{1}{a}\tan^{-1}\left(\frac{x}{a}\right)
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\int\frac{1}{x^2 - a^2}\;\mathrm{d}x &= \frac{1}{2a}\ln\left|\frac{x-a}{x+a}\right|
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\int\frac{1}{\sqrt{a^2 - x^2}}\;\mathrm{d}x &= \sin^{-1}\left(\frac{x}{a}\right),\;a>0
\end{split}
\end{equation}$$
$$\begin{equation}
\begin{split}
\int\frac{1}{\sqrt{x^2 \pm a^2}}\;\mathrm{d}x &= \ln\left|x+\sqrt{x^2\pm a^2}\right|
\end{split}
\end{equation}$$
Riemann Sums
Given
$$\begin{equation}
\begin{split}
A &= \int_{a}^{b} f(x) = \lim_{n\to\infty}\sum_{i=1}^{n} \Delta{x} \cdot f(x) \;\text{where}\;
\left\{\begin{array}{ll}
\Delta{x} = \frac{b - a}{n}
\end{array}\right.
\end{split}
\end{equation}$$
Left Riemann Sum
$$\begin{equation}
\begin{split}
A &= \int_{a}^{b} f(x) \;\mathrm{d}x \approx L_n = \sum_{i = 0}^{n-1}\, \Delta{x}\cdot f\left(a + i\cdot\Delta{x}\right)
\end{split}
\end{equation}$$
Right Riemann Sum
$$\begin{equation}
\begin{split}
A &= \int_{a}^{b} f(x) \;\mathrm{d}x \approx R_n = \sum_{i = 1}^{n}\, \Delta{x}\cdot f\left(a + i\cdot\Delta{x}\right)
\end{split}
\end{equation}$$
Midpoint Riemann Sum
$$
\newcommand{\generalFormat}{
\sum_{\small{\cdots}}^{\small{\cdots}}\, \Delta{x}\cdot f\left(a + \text{“avg. of $x_i$ and $x_{i-1}$”} \cdot \Delta{x}\right)
}
\newcommand{\SigmaExampleOne}{
\sum_{i = 1}^{n}\, \Delta{x}\cdot f\left(a + \frac{x_{i - 1} + x_i}{2} \cdot \Delta{x}\right)
}
\newcommand{\SigmaExampleTwo}{
\sum_{i = 0}^{n-1}\, \Delta{x}\cdot f\left(a + \frac{x_{i + 1} + x_i}{2} \cdot \Delta{x}\right)
}
\begin{equation}
\begin{split}
A = \int_{a}^{b} f(x) \;\mathrm{d}x &\approx \generalFormat\\
&\approx \SigmaExampleOne\\
\text{or alternatively}&\\
A &\approx \SigmaExampleTwo
\end{split}
\end{equation}
$$
We can also do away with the index notation and simplify things.
$$
\newcommand{\SigmaExampleOne}{
\sum_{i = 1}^{n}\, \Delta{x}\cdot f\left(a + \frac{(i - 1) + i}{2} \cdot \Delta{x}\right) =
\sum_{i = 1}^{n}\, \Delta{x}\cdot f\left(a + \frac{2i - 1}{2} \cdot \Delta{x}\right)
}
\newcommand{\SigmaExampleTwo}{
\sum_{i = 0}^{n-1}\, \Delta{x}\cdot f\left(a + \frac{(i + 1) + i}{2} \cdot \Delta{x}\right) =
\sum_{i = 0}^{n-1}\, \Delta{x}\cdot f\left(a + \frac{2i + 1}{2} \cdot \Delta{x}\right)
}
\begin{equation}
\begin{split}
A = \int_{a}^{b} f(x) \;\mathrm{d}x
&\approx \SigmaExampleOne\\
&\approx \SigmaExampleTwo
\end{split}
\end{equation}
$$
Trapezoidal Riemann Sum
$$
\dots
$$
Simpson's Rule
$$\begin{equation}
\begin{split}
\dots
\end{split}
\end{equation}$$
Improper Integrals
$$\begin{equation}
\begin{split}
\text{Given}&\;L = \int_{a}^{\infty} f(x) \;\mathrm{d}x = \lim_{t\to\infty} \int_{a}^{\infty} f(x) \;\mathrm{d}x = \lim_{t\to\infty} F(x)\\
\text{If}&\;L\;\text{“exists”}\;\text{then $L$ is}\;\mathbf{\text{convergent}}\\
\text{If}&\;L\;\text{“does not exists”}\;\text{then $L$ is}\;\mathbf{\text{divergent}}
\end{split}
\end{equation}$$
Infinite Sequences
Infinite Sequence
$$\begin{equation}
\begin{split}
\text{Given}&\\
&S_n = \{a_n\}_{n=1}^{\infty}\\
\text{Tests}&\\
&\text{If}\;\lim_{n\to\infty}\,S_n \text{“exists”}\;\text{then}\;\mathbf{\text{$S_n$ is convergent}}\\
&\text{If}\;\lim_{n\to\infty}\,S_n \text{“does not exists”}\;\text{then}\;\mathbf{\text{$S_n$ is Divergent}}\\
\end{split}
\end{equation}$$
Helpful Theorem
$$\begin{equation}
\begin{split}
\text{If}&\\
\lim_{x\to\infty}\,|a_n| &= 0\\
\text{Then}&\\
\lim_{x\to\infty}\,a_n &= 0\\
\end{split}
\end{equation}$$
Example
$$\begin{equation}
\begin{split}
\text{Given}\\
S_n &= \{\cos\left(\frac{n\pi}{2}\right)\}\\
L &=\lim_{n\to\infty}\,\cos\left(\frac{n\pi}{2}\right)\\
&= \cos\left(\lim_{n\to\infty}\,\frac{n\pi}{2}\right) \\
&= \cos\left(\infty\right) \\
&= \text{undefined} \\
\text{Therefore}\\
\therefore\;&\text{$S_n$ is Divergent}&
\end{split}
\end{equation}$$
Example
$$\begin{equation}
\begin{split}
\text{Given}\\
S_n &= \{\sin\left(\frac{\pi}{n}\right)\}\\
L &= \lim_{n\to\infty}\,\sin\left(\frac{\pi}{n}\right)\\
&= \sin\left(\lim_{n\to\infty}\,\frac{\pi}{n}\right) \\
&= \sin\left(0\right) \\
&= 0\\
\text{Therefore}\\
\therefore\;&\text{$S_n$ is Convergent}
\end{split}
\end{equation}$$
Infinite Series
Infinite Series
$$\begin{equation}
\begin{split}
\text{Given}&\\
&S_n = \sum_{n = 1}^{\infty}\,a_n\\
\text{Tests}&\\
&\text{If}\;\lim_{n\to\infty}\,a_n = 0\;\text{then}\;\text{$S_n$ may be $\mathbf{\text{convergent}}$}\\
&\text{If}\;\lim_{n\to\infty}\,a_n \neq 0\;\text{then}\;\mathbf{\text{$S_n$ is divergent}}\\
&\text{If}\;\lim_{n\to\infty}\,a_n \text{“does not exists”}\;\text{then}\;\mathbf{\text{$S_n$ is divergent}}\\
\end{split}
\end{equation}$$
Note that the limit of every convergent series is equal to zero. But the inverse isn't always true. If the limit is equal to zero, it may not be convergent.
For example, \(\sum_{n=1}^\infty \frac{1}{n}\) does diverge; but it's limit is equal to zero.
If the limit is equal to zero; the test is inconclusive.
Geometric Series
$$\begin{equation}
\begin{split}
\text{Given}&\\
&S_n = \sum_{n = 1}^{\infty}\,a_n = \sum_{n = 1}^{\infty}\,a\cdot r^{n - 1}\;\text{where}\;
\left\{\begin{array}{ll}
\begin{split}
a &= a_1\\
r &= \frac{S_2}{S_1}
\end{split}
\end{array}\right.\\
\text{Alternatively}&\\
&S_n = \sum_{n=0}^{\infty}\,a_n = \sum_{n=0}^{\infty}\,a\cdot r^{n}\\
\text{Tests}&\\
&\text{If}\;|r|\geq{1}\;\text{then}\;\mathbf{\text{$S_n$ is divergent}}\\
&\text{If}\;|r|<1\;\text{then}\;\mathbf{\text{$S_n$ is convergent}}\\
\text{Furthermore}&\\
&\sum_{n = 1}^{\infty}\,a_n = \sum_{n = 1}^{\infty}\,a\cdot r^{n - 1} = \frac{a}{1 - r}\;\text{for all}\;|r|<1
\end{split}
\end{equation}$$
The Integral Test
$$\begin{equation}
\begin{split}
&\text{Given}\\
&\;\;\;\;a_n = f(n)\;\text{$\forall$n on}\;[1,n)\\
&\;\;\;\;S_n = \sum_{n = 1}^{\infty}\,a_n\\
&\;\;\;\;F(x) = \int_{1}^{\infty}f(x)\;\mathrm{d}x\\
&\text{Where}\\
&\;\;\;\;f(x) > 0, \forall\,x\in\,[1, \infty)\\
&\;\;\;\;f^\prime(x) < 0, \forall\,x\in\,[1, \infty)\\
&\text{Tests}\\
&\;\;\;\;\text{If $S_n$ convergent; then $F(x)$ is $\mathbf{convergent}$}\\
&\;\;\;\;\text{If $S_n$ divergent; then $F(x)$ is $\mathbf{divergent}$}
\end{split}
\end{equation}$$
Constraints on \([1,n)\)
- Continuous
- Positive
- Decreasing (i.e. use derivative test)
P-Series -or- Harmonic Series
$$\begin{equation}
\begin{split}
&\text{Given}\\
&\;\;\;\;S_n=\sum_{n=1}^{\infty}\frac{1}{n^p}\\
&\text{Tests}\\
&\;\;\;\;\text{If $p>1$ then $S_n$ is $\mathbf{convergent}$}\\
&\;\;\;\;\text{If $0 < p \leq{1}$ then $S_n$ is $\mathbf{divergent}$}
\end{split}
\end{equation}$$
Note: the Harmonic series is the special case where \(p=1\)
Comparison Test
$$\begin{equation}
\begin{split}
&\text{Given}\\
&\;\;\;\;A_n = \sum_{n=1}^\infty\,a_n\\
&\;\;\;\;B_n = \sum_{n=1}^\infty\,b_n\\
&\text{Where}\\
&\;\;\;\;a_n, b_n \geq 0\\
&\;\;\;\;a_n \leq b_n\\
&\text{Tests}\\
&\;\;\;\;\text{If $B_n$ converges $\implies A_n$ converges}\\
&\;\;\;\;\text{If $A_n$ diverges $\implies B_n$ diverges}\\
\end{split}
\end{equation}$$
Limit Comparison Test
$$\begin{equation}
\begin{split}
&\text{Given}\\
&\;\;\;\;A_n = \sum_{n=1}^\infty\,a_n\\
&\;\;\;\;B_n = \sum_{n=1}^\infty\,b_n\\
&\;\;\;\; L = \lim_{n\to\infty}\frac{a_n}{b_n}\\
&\text{Where}\\
&\;\;\;\;L > 0,\;L \neq \pm \infty\\
&\text{Therefore either both converge or diverge}\\
&\;\;\;\;\text{$A_n$ converges $\Longleftrightarrow B_n$ converges}\\
&\;\;\;\;\text{$A_n$ diverges $\Longleftrightarrow B_n$ diverges}
\end{split}
\end{equation}$$
Warning
- If \(L > 0\), this only means that the limit comparison test can be used. You still need to determine if either\(A_n\) or \(B_b\) converges or diverges.
- Therefore, this does not apply to any arbitrary rational function.
Notes
- For many series, we find a suitable comparison, \(B_n\), by keeping only the highest powers in the numerator and denominator of \(A_n\).
Estimating Infinite Series
$$\begin{equation}
\begin{split}
\cdots
\end{split}
\end{equation}$$
Differential Equations
Separable Differential Equations
$$\begin{equation}
\begin{split}
\text{Given}\\
\frac{\mathrm{d}y}{\mathrm{d}x}
&= g(x) \cdot f(y)\\
&= \frac{g(x)}{\frac{1}{f(y)}}\\
&= \frac{g(x)}{h(y)}\;\text{where}\;h(x) = \frac{1}{f(y)}\\
\\\text{Therefore (restated)}\\
\frac{\mathrm{d}y}{\mathrm{d}x} &= \frac{g(x)}{h(y)}\\
\\\text{Multiply reciprocals}\\
h(y)\;\mathrm{d}y &= g(x)\;\mathrm{d}x\\
\\\text{Integrate}\\
\int h(y)\;\mathrm{d}y &= \int g(x)\;\mathrm{d}x\\
\\\text{Differentiate}\\
\frac{d}{dx} \left(\int h(y)\;\mathrm{d}y\right) &= \frac{d}{dx} \left(\int g(x)\;\mathrm{d}x\right)\\
\\\text{Given}\\
\frac{\mathrm{d}}{dx}
&= \frac{\mathrm{d}}{dx} \cdot \frac{\mathrm{d}y}{\mathrm{d}y}
= \textcolor{blue}{\frac{\mathrm{d}}{dy}} \cdot \textcolor{JungleGreen}{\frac{\mathrm{d}y}{dx}}\\
\\\text{Therefore the LHS is equal to}\\
\frac{\mathrm{d}}{dx} \left(\int h(y) \mathrm{d}y\right)
&= \textcolor{blue}{\frac{\mathrm{d}}{dy}} \left(\int h(y) \mathrm{d}y\right) \textcolor{JungleGreen}{\frac{\mathrm{d}y}{dx}}\\
&= h(y) \textcolor{JungleGreen}{\frac{\mathrm{d}y}{dx}}
\\\text{Therefore (in conclusion)}\\
\therefore \; h(y)\;\frac{\mathrm{d}y}{dx} &= g(x)
\end{split}
\end{equation}$$
Growth and Decay Models
$$\begin{equation}
\begin{split}
\text{Given}\\
\frac{\mathrm{d}y}{\mathrm{d}t} &= \textcolor{Periwinkle}{k} y\\
\text{Proof}\\
\frac{1}{y}\;\mathrm{d}y &= \textcolor{Periwinkle}{k}\;\mathrm{d}t \\
\int \frac{1}{y}\;\mathrm{d}y &= \int \textcolor{Periwinkle}{k}\;\mathrm{d}t \\
\ln(y) &= \textcolor{Periwinkle}{k} t + \textcolor{SeaGreen}{C} \\
e^{\ln(y)} &= e^ {\textcolor{Periwinkle}{k} t + \textcolor{SeaGreen}{C}} \\
y &= e^{\textcolor{Periwinkle}{k} t} \cdot e^{\textcolor{SeaGreen}{C}} \\
y &= e^{\textcolor{Periwinkle}{k} t} \cdot \textcolor{SeaGreen}{C} \\
\text{Therefore}\\
y &= \textcolor{SeaGreen}{C} e^{\textcolor{Periwinkle}{k} t}
\end{split}
\end{equation}$$
The above states that all solutions for \(y^\prime = k y\) are of the form \(y = C e^{k t}\).
Where
$$\begin{equation}
\begin{split}
\textcolor{SeaGreen}{C} &= \textcolor{SeaGreen}{\text{Initial value of $y$}}\\
\textcolor{Periwinkle}{k} &= \textcolor{Periwinkle}{\text{Proportionality constant}}\\
\end{split}
\end{equation}$$
Exponential growth occurs when \(\textcolor{Periwinkle}{k > 0}\), and exponential decay occurs when \(\textcolor{Periwinkle}{k < 0}\).
The Law of Natural Growth:
$$\begin{equation}
\begin{split}
\frac{\mathrm{d}\textcolor{DarkOrchid}{P}}{\mathrm{d}t}
= \textcolor{Periwinkle}{k} \textcolor{DarkOrchid}P
\end{split}
\end{equation}$$
The Logistic Model of Population Growth:
$$\begin{equation}
\begin{split}
\frac{\mathrm{d}\textcolor{DarkOrchid}P}{\mathrm{d}t}
= \textcolor{Periwinkle}{k} \textcolor{DarkOrchid}P
\left(1 - \frac{\textcolor{DarkOrchid}{P}}{\textcolor{Aquamarine}{L}}\right)
\end{split}
\end{equation}$$
Where
$$\begin{equation}
\begin{split}
\textcolor{Periwinkle}{k} &= \textcolor{Periwinkle}{\text{Constant of proportionality}}\\
\textcolor{DarkOrchid}{P} &= \textcolor{DarkOrchid}{\text{Population at time $t$}}\\
\textcolor{Aquamarine}{L} &= \textcolor{Aquamarine}{\text{Max size of population}}\\
\end{split}
\end{equation}$$
Solving the Logistic Equation
$$\begin{equation}
\begin{split}
\D{P}{t} &= kP \parens{1 - \frac{P}{L}} \\
\s{d}P &= kP \parens{1 - \frac{P}{L}} \s{d}t \\
\reciprocal{P \parens{1 - \frac{P}{L}}} \s{d}P &= k \s{d}t
\end{split}
\end{equation}$$
Via partial fraction decomposition
$$\begin{equation}
\begin{split}
\reciprocal{P \parens{1 - \frac{P}{L}}} &= \frac{A}{P} + \frac{B}{\parens{1 - \frac{P}{L}}}\\
0P + 1 &= A\parens{1 - \frac{P}{L}} + BP\\
0P + 1 &= A - \frac{P A}{L} + BP\\
0P + 1 &= P\parens{B - \frac{A}{L}} + A \\
\text{Where}\\
\left.\begin{array}{ll}
B - \frac{A}{L} &= 0\\
A &= 1
\end{array}\right\}
\;\begin{array}{ll}
A &= 1\\
B &= \reciprocal{L}
\end{array}\\
\text{Therefore}\\
\reciprocal{P \parens{1 - \frac{P}{L}}} &= \frac{1}{P} + \frac{\reciprocal{L}}{\parens{1 - \frac{P}{L}}}
\end{split}
\end{equation}$$
Rewriting the differential equation
$$\begin{equation}
\begin{split}
\reciprocal{P \parens{1 - \frac{P}{L}}} \s{d}P
&= \frac{1}{P} + \frac{\reciprocal{L}}{\parens{1 - \frac{P}{L}}} \s{d}P\\
&= k \s{d}t \\
\int \frac{1}{P} + \frac{\reciprocal{L}}{\parens{1 - \frac{P}{L}}}
&= \int k \s{d}t \\
\ln\; P - \reciprocal{L} \ln\parens{1 - \frac{P}{L}} &= k t + C\\
\ln\parens{\frac
{P}
{L \cdot \parens{1 - \frac{P}{L}}}
}
\end{split}
\end{equation}$$
Second Order Homogeneous Linear Differential Equations with Constant Coefficients
Properties
-
If \(f(x)\) and \(g(x)\) are solutions; then \(f + g\) is also a solution. Therefore, the most general solution to some second order homogeneous linear differential equations with constant coefficients would be \(y = C_1 f(x) + C_2 g(x)\).
This is why, when you find two solutions to the characteristic equation \(r_1\) and \(r_2\) respectively, we write it like so.
\(r_1 = r_2\)
Given some:
$$\begin{equation}
\begin{split}
a y^{\prime\prime} + b y^\prime + c y = 0\;\text{where $a \neq 0$}\\
\end{split}
\end{equation}$$
We can presume that \(y\) is of the form \(e^{r t}\), and therefore:
$$\begin{equation}
\begin{split}
\text{if}\\
y &= e^{r t}\\
\text{then}\\
y^{\prime} &= r e^{r t}\\
y^{\prime\prime} &= r^2 e^{r t}
\end{split}
\end{equation}$$
Substituting this back into the original equation, we have:
$$\begin{equation}
\begin{split}
0 &= a r^2 e^{r t} + b r e^{r t} + c e^{r t}\\
&= e^{r t} \left(a r^2 + b r + c\right)
\end{split}
\end{equation}$$
Where:
$$\begin{equation}
\begin{split}
&= \underbrace{e^{r t}}_\text{never $0$}
\underbrace{\left(a r^2 + b r + c\right)}_\text{?}
\end{split}
\end{equation}$$
So therefore:
$$\begin{equation}
\begin{split}
&\underbrace{a r^2 + b r + c = 0}
_\text{characteristic equation}\\
&r = \frac
{-b \pm \sqrt{b^2 - 4ac}}
{2a}
\implies r_1, r_2
\end{split}
\end{equation}$$
Where the general solution is of the form:
$$\begin{equation}
\begin{split}
\left.
\begin{array}{ll}
y &=\; &C_1\; e^{r_1 t} &+\; C_2\; e^{r_2 t}\\
y^\prime &=\; &C_1\; r_1\; e^{r_1 t} &+\; C_2\; r_2\; e^{r_2 t}\\
y^{\prime\prime} &=\; &C_1\; \left(r_1\right)^2\; e^{r_1 t} &+\; C_2\; \left(r_2\right)^2\; e^{r_2 t}
\end{array}
\right\}\text{$\forall r_1 \; r_2$ where $r_1 \neq r_2$}
\end{split}
\end{equation}$$
Parametric Equations
First Derivative Formula
To find the derivative of a given function defined parametrically by the equations \(x = u(t)\) and \(y = v(t)\).
$$\begin{equation}
\begin{split}
\text{Given}\\
x &= u(t)\\
y &= v(t)\\
\text{Therefore}\\
\frac{\mathrm{d}y}{\mathrm{d}x}
&= \frac
{\frac{\mathrm{d}y}{\mathrm{d}t}}
{\frac{\mathrm{d}x}{\mathrm{d}t}}
= \frac{v^\prime(t)}{u^\prime(t)}
\end{split}
\end{equation}$$
Second Derivative Formula
To find the second derivative of a given function defined parametrically by the equations \(x = u(t)\) and \(y = v(t)\).
$$\begin{equation}
\begin{split}
\text{Given}\\
x &= u(t)\\
y &= v(t)\\
\text{Therefore}\\
\frac{\mathrm{d}{^2} y}{\mathrm{d}x^2}
&= \frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{\mathrm{d}y}{\mathrm{d}x}\right)\\
&= \frac
{
\frac{d}{\mathrm{d}t}\left( \frac{\mathrm{d}y}{\mathrm{d}x} \right)
}
{\frac{\mathrm{d}x}{\mathrm{d}t}}\\
&= \frac
{
\frac{\mathrm{d}}{\mathrm{d}t}
\left(\frac{v^\prime(t)}{u^\prime(t)}\right)
}
{u^\prime(t)}\\
&= \underbrace
{
\frac
{
\frac{\mathrm{d}}{\mathrm{d}t}
\left(\frac{v^\prime(t)}{u^\prime(t)}\right)
}
{
\frac{\mathrm{d}}{\mathrm{d}t}
u(t)
}
= \frac
{
\frac{\mathrm{d}}{\mathrm{d}t}
}
{
\frac{\mathrm{d}}{\mathrm{d}t}
}
\frac
{
\left(\frac{v^\prime(t)}{u^\prime(t)}\right)
}
{
u(t)
}
}_{\text{notice the common $\frac{\mathrm{d}}{\mathrm{d}t}$}}
\end{split}
\end{equation}$$
The above shows different ways of representing \(\frac{\mathrm{d}^{2}y}{\mathrm{d}x^2}\). (I.e. it doesn't correspond to some final solution.)
Arc Length
Formula for the arc length of a parametric curve over the interval \([a, b]\).
$$\begin{equation}
\begin{split}
\int_a^b \sqrt{
\left(\frac{\mathrm{d}x}{\mathrm{d}t}\right)^2 +
\left(\frac{\mathrm{d}y}{\mathrm{d}t}\right)^2
}
\mathrm{d}t
\end{split}
\end{equation}$$